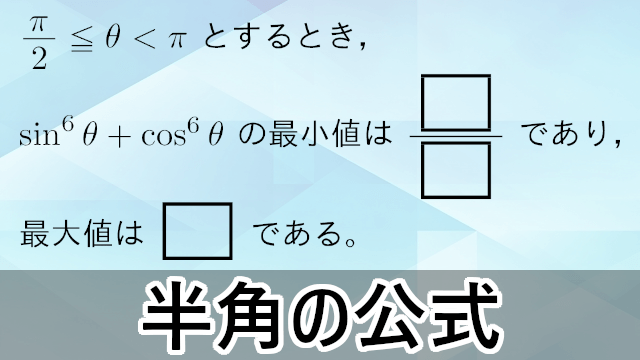
2倍角の公式と半角の公式 タイプ: 教科書範囲 レベル: ★★ 三角関数の2倍角の公式と半角の公式を紹介し,演習問題を用意しました. これらは 加法定理 から導けることが重要ですが,頻繁に登場するので是非覚えましょう. 目次 1: 2倍角の公式と半角の公式の使い方 半角の公式は、 θ の三角関数を使って θ 2 の三角関数の値を求めたい! というときに使えます。 半角の公式を使う例題: (1) tan 15 ∘ を求めよ。 解答: 半角の公式: <三倍角の公式と半角の公式> ※ちなみに、 tanの半角も相互関係を使って 、$$\tan の半角公式=\frac {\sin の半角}{\cos の半角}$$で導けるので、特に流れを覚えておく必要はありません。 半角公式のもう一つの導き方(重要!)
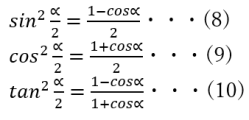
三角関数 加法定理およびその他の派生公式の覚え方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
半角の公式 覚え方
半角の公式 覚え方- 応用分野: 三角方程式の解き方, 積分 1/(sinx)^4, 積分 1/(cosx)^4, 式の導出, 式の導出, 加法定理, 続きを見る 問題リスト ←このページに関連している問題です「半角の公式の覚え方や、使う場面が知りたい! 確実に解が求まる2倍角の公式の効率的な覚え方→ 半角の公式の覚え方語呂合わせ 半角の公式は二倍角の公式から簡単に導けるため(やり方はコチラ)、わざわざ語呂で覚える必要はありません。 ですが、「毎回導くのは嫌だから暗記してしまいたい!」という人向けに、半角の公式の語呂合わせを \(1
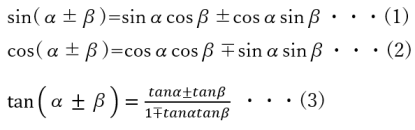



三角関数 加法定理およびその他の派生公式の覚え方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
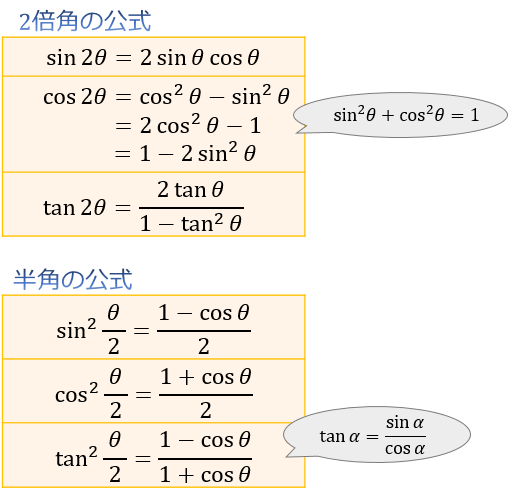
半角の公式|覚え方 半角の公式は のように で書くこともあれば、 で書くこともあります。 僕個人としては 後者の方を覚えることをオススメ します。 2倍角から簡単に導出できますし、問題で利用する際には後者の方が使いやすいです。 楓 を に この公式の利点は 次数を2から1に 下げることができる という点にあります。 次数を下げた方がいいかどうかは 適宜自分で判断するしかありませんが、 とにかく 半角の公式は 三角関数の次数を 下げることができる という点は覚えておきましょう。Contents• ぜひ最後まで読んで、半角を完璧にマスターしましょう! 半角公式は、加法定理や倍角の公式などを基本としています。 1:二倍角の公式の覚え方(語呂合わせ) まずは二倍角の公式の一覧と二倍角の公式の覚え方(語呂合わせ)を紹介します。
3倍角の公式と覚え方 sinとcosは語呂合わせで覚えるのがいいと思います。 tanはあまり良い語呂合わせがないので頑張って覚えてください。 sinとcosはtanよりも使う機会が多いような気がします。難関大学受験者は必ず3つとも覚えておきましょう。「数学Ⅱ|三角関数」の公式まとめです。 (下の方に練習問題があります。 半角 和積の公式 それでは公式を覚えたか、練習問題で確認してみましょう。約2年前 倍角と半角公式は、ふつうに加法定理から3秒ぐらいで導けるのでわざわざ語呂合わせするのはむしろ効率が悪いかと この回答にコメントする にゃんこ 約2年前 調べれば出てくるかも? っことより、 加法定理を覚えていれば問題ないでしょう
加法定理の覚え方。図形でわかる公式 二等辺三角形で分かる2倍角の考え方 今回は、2倍角の公式と半角の公式について書いていきます。 3倍角公式という覚え方があるので利用してみると良いです。 この公式はもちろん導出できるものですが、 覚えてしまった方が簡単なので導出までしっかり理解しておく必要はあまりないです。 倍角の公式 \begin{eqnarray} \Large \sin 2\theta &\Large=& \Large 2\sin \theta \cos \thetaこのページでは、数学Ⅱの「三角関数の公式」をまとめました。 三角関数の公式と覚え方を、わかりやすく解説していきます。 問題集を解く際の参考にしてください! 目次1 三角関数の公式11 三角関数の変



三角関数 プログレス進学塾 看護学校 看護大学受験の専門



2倍角の公式とは 1分でわかる意味 求め方 問題 倍角の意味 証明
2倍角の公式 1 2 3 tan2 1 cos 21 1 cos cos 2 α αα α − = ゆえに 22 2 2 1 2 3 1 cos 1 cos 2 3 2 2 22 2 2 2 2 2 2 1 2sin 2tan sin 2sin cos cos tan 2cos 1 1 tan sin cos ta α αα α αα α α αα α αα − − === − − = は、以下のようにも使われます。 は、以下のようにも使われます。 1 この公式から2倍角や半角の公式が導けるので、 いざ公式をを忘れたとき導出できるようにしておきましょう 楓 半角の公式覚え方 半角の公式は のように\(\frac{\theta}{2}\)で書くこともあれば、\(\theta\)で書くこともあります。 半角の公式 半角の公式の覚え方 上の図の公式を覚えましょう。 今回の公式は、暗記ではなくても簡単に導き出すことができ、同時に証明もでき圧倒的に役立つので、それぞれ加法定理から導き出すことができるまで何回も練習しましょう。 半角の公式の証明



1から半角の公式の覚え方 使い方を解説 数学2bの苦手を克服 Studyplus スタディプラス




半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法
半角の公式の効率的な覚え方と、証明、使える場面→次数を調整したい 青春マスマティック 鴨宮かのや酒店 神奈川県小田原市 2倍角と半角の公式って語呂合わせありますか? 導き方をおさえた上で暗記が必要である。 三角関数の2倍角の公式・半角の公式の証明と応用 2zh 問題演習する中で自然に覚えてしまうのが理想だが,\ それが無理ならば丸暗記したほうがよい \\2zh 特に,\ \bm{\cos2\alpha\,の公式は,\ 3通りの表現を全て 数学の公式の覚え方 ここでは、数学の公式の覚え方について5つの方法を解説していきます。どの方法もかなり効果的なので、ぜひ試してもらえればと思います。 まずは公式の意味を理解する 数学の公式を覚える際は、まず 「公式の意味を理解する




受験数学かずスクール 加法定理 二倍角 半角 三倍角 和積 積和など三角関数の公式の覚え方 扱い方




Trigger Trigger Twitter
ズボラ公式記憶法三角関数 半角の公式の動画を更新しました。 動画では、覚えなくていいこともお教えします。 ズボラして、覚えるものを少なくすればするほど、 勘違いがおきない正確な記憶になります。 ズボラ半角/二倍角の公式の覚え方は「覚えない事」!?その重要な意味と方法 😁 高校生の苦手解決q&aは,自分で公式を導けるようになることが重要です。 下のボタンから、無料体験のお申込みが可能です。半角の公式とは、角 α/2 の三角関数を、角 α の三角関数の形に変換する公式です。このページでは、sin, cos, tan の半角の公式を示しています。また、これらの公式の導出方法と、計算例も説明していま



1




半角の公式 覚え方 導き方 理系ラボ
半角 の 公式 覚え 方 半角 の 公式 覚え 方2倍角の公式 半角の公式とその証明 二等辺三角形で分かる2倍角の考え方 アタリマエ For more information and source, 半角の公式 の効率的な覚え方と 証明 使える場面 次数を調整したい 青春マスマティック For more information→ 印刷用pdf版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「加法定理は覚える,他は作る」というのが,作者おすすめの考え方です。・・・ただし,そういう公式があるということと,およその形は記憶にとどめます。半角公式は,次の形で示されることもある.±は,象限に応じて一方の符号を選ぶことを表わす. を で表すのと, を で表わすのとでは,対応関係は同じだから,好きな方を使えばよい.




3分で分かる 半角公式の覚え方と証明 使い方のコツ 合格サプリ




加法定理の覚え方を5つ紹介 これでテストでも困らない




2倍角の公式と半角の公式 おいしい数学




の部分の式変換が分からないので 途中式を含めて教えていただきたいです Clear



写真のような公式や二倍角 半角の公式の良い覚え方とかってありま Yahoo 知恵袋




1分で覚える ゴロ合わそんぐ 半角の公式 社長にばれるとヤバイヤバイ Youtube




高2 加法定理は語呂合わせで完ペキに暗記 高校生 数学のノート Clearnote
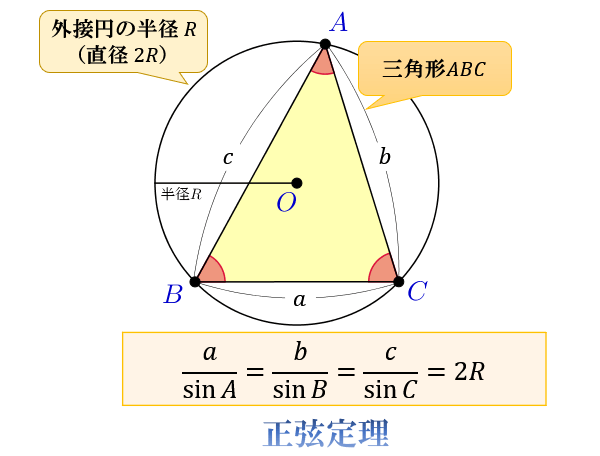



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




半角の公式の覚え方 自宅を自習室に 医進館に
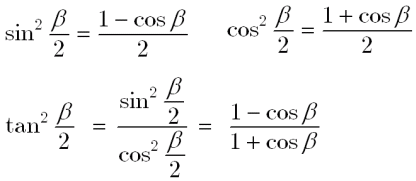



三角比 倍角の公式 半角の公式 大人が学び直す数学




半角の公式 の効率的な覚え方と 証明 使える場面 次数を調整したい 青春マスマティック




高校数学 三角関数の2倍角の公式 半角の公式の証明と応用 受験の月
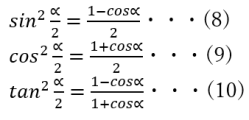



三角関数 加法定理およびその他の派生公式の覚え方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




半角の公式とは 覚え方 語呂合わせ や証明 問題での使い方 受験辞典




3倍角の公式の覚え方をマスターしよう 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




たった6つの公式から三角関数の公式を全て導く方法 塾講師ステーション情報局



2倍角の公式 半角の公式とその証明 二等辺三角形で分かる2倍角の考え方 アタリマエ



和積 積和 倍角 半角の公式 理数系無料オンライン学習 Kori




半角の公式 覚え方 導き方 理系ラボ




高校数学b S公式 問題一覧 公式 覚え方 計算方法 学校よりわかりやすいサイト




1分で覚える ゴロ合わそんぐ 三倍角の公式 Youtube




加法定理の覚え方を5つ紹介 これでテストでも困らない




かんたん最強の数学 半角の公式の覚え方 加法定理 こっそりと入試で役立つ裏技も紹介します Youtube



三角関数 加法定理 時習館 ゼミナール 高等部




2倍角の公式 覚え方 導き方 理系ラボ




三角関数 加法定理 2倍角 半角の公式 富岡市の総合学習塾 トータルアカデミー




二倍角 三倍角公式 半角公式 理系ノート




二倍角の公式の覚え方 語呂合わせ 即覚えられる 高校生向け受験応援メディア 受験のミカタ




半角の公式の覚え方や使い方を徹底解説




Tan二倍角公式 2倍角の公式 覚え方 導き方 Elleve




半角の公式の使い方 導出 覚え方 具体例で学ぶ数学




4fmgwgonmmdwzm



1




半角の公式の使い方 導出 覚え方 具体例で学ぶ数学
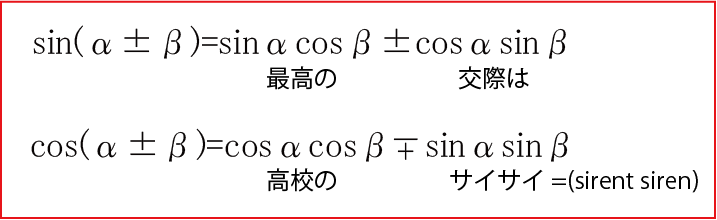



加法定理とは 公式と証明 簡単な覚え方を語呂合わせで説明します 高校生向け受験応援メディア 受験のミカタ



1から半角の公式の覚え方 使い方を解説 数学2bの苦手を克服 Studyplus スタディプラス




半角の公式



加法定理とは 公式と証明 簡単な覚え方を語呂合わせで説明します 高校生向け受験応援メディア 受験のミカタ




半角の公式 覚え方 導き方 理系ラボ



Aqgsxd4q4z Pqm




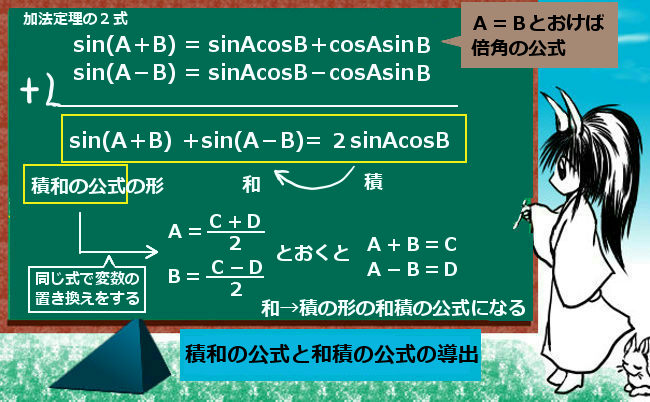
和積 積和の公式のわかりやすい覚え方と証明のコツ
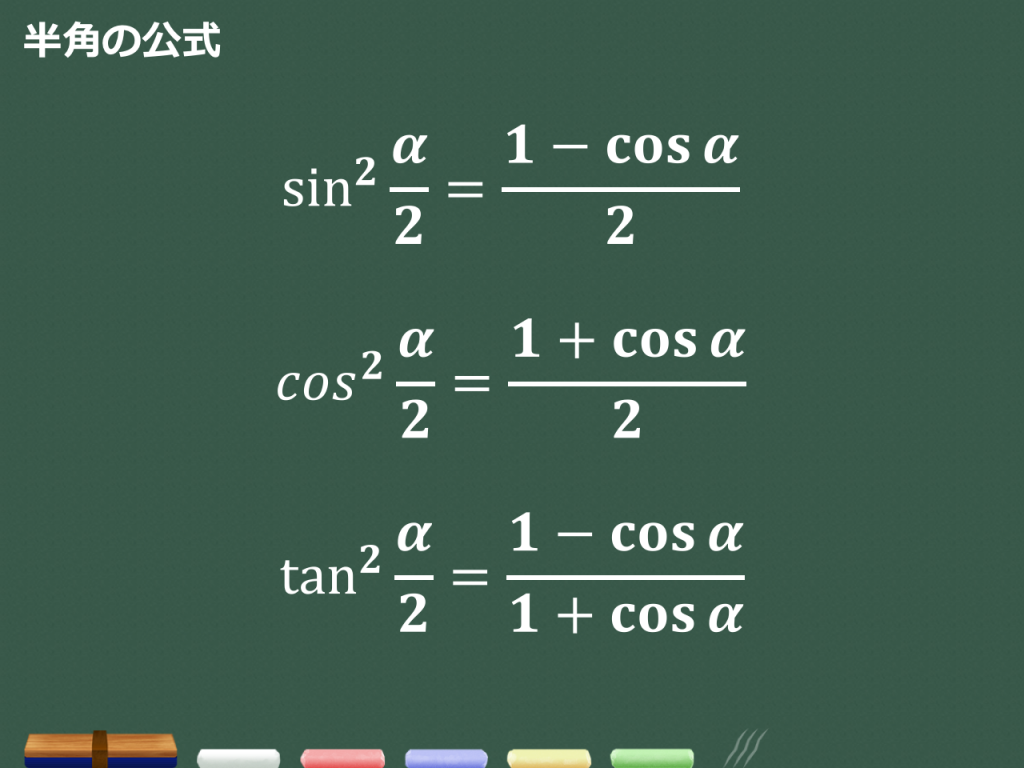



3分で分かる 半角公式の覚え方と証明 使い方のコツ 合格サプリ



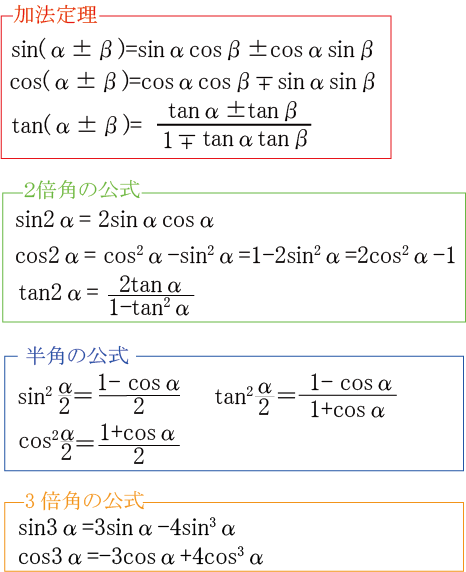
三角関数 加法定理およびその他の派生公式の覚え方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




3分で分かる 2倍角の公式の覚え方と証明 使い方をわかりやすく 合格サプリ



1から半角の公式の覚え方 使い方を解説 数学2bの苦手を克服 Studyplus スタディプラス




半角の公式の覚え方 自宅を自習室に 医進館に




予備校講師がアドバイス 数学の公式の覚え方 子どものための教育支援情報サイト スタディメンター




3分で分かる 半角公式の覚え方と証明 使い方のコツ 合格サプリ




半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法




高2 加法定理は語呂合わせで完ペキに暗記 高校生 数学のノート Clearnote




高校数学 半角の公式とは 映像授業のtry It トライイット




三角関数 加法定理 2倍角 半角の公式 富岡市の総合学習塾 トータルアカデミー




3倍角の公式の覚え方をマスターしよう 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



1



1




三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要




数学 三角関数の公式まとめ 加法定理 変換 合成 理系ラボ
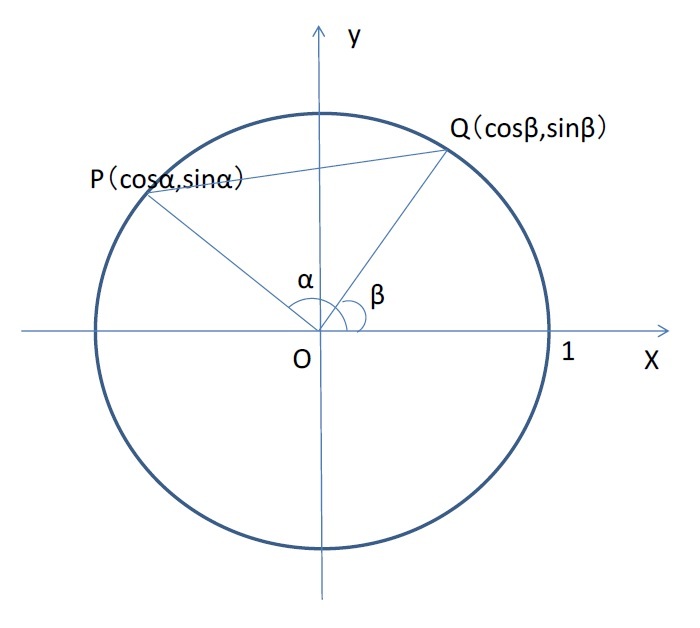



三角関数 の基本的な定理とその有用性を再確認してみませんか その2 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所




半角公式が一目でわかる 証明 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ




半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法




無料印刷可能公式 数学 壁紙 最高の花の画像



数学 B 三角関数の半角の公式 関西大 慶應義塾大 星薬科大 大学入試数学の考え方と解法



加法定理 二倍角 半角の公式の覚え方 簡単な覚え方 覚えやすい覚 Yahoo 知恵袋




半角 3倍角 和の公式は覚えておいた方がいいですか Clearnote




数学 半角の公式は覚えるな Youtube



三角関数の公式が覚わりません 二倍角 半角が特に 何か語呂合 Yahoo 知恵袋




数学検定1級合格者が解説 三角関数 半角の公式を覚える 一瞬で覚える語呂合わせ 公式を覚えよう 数検 Youtube




日本一簡単に覚えられる 加法定理 倍角 半角 3倍角の公式 高校数学 三角関数 Youtube



三角関数 入試頻度は星三つ判定 が多いほど頻出 1 相互関係によるこの3つの公式は 様々な問題で使いますので 絶対覚えてください 2 有名な加法定理の公式です 加法定理の覚え方は いろんなサイトで公開されてますが




半角の公式と証明 導き方を解説 もう公式を忘れても大丈夫




高校数学 三角関数の3倍角の公式の証明とゴロ合わせ 受験の月




2倍角 半角 3倍角の公式の作り方 覚え方 Youtube




加法定理とは 公式と証明 簡単な覚え方を語呂合わせで説明します 高校生向け受験応援メディア 受験のミカタ




3倍角の公式の覚え方 ゴロ 自宅を自習室に 医進館に




三角関数の公式の一覧 Wikipedia
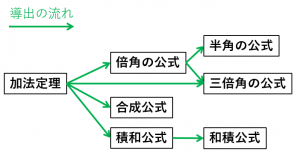



三角関数の加法定理に関する公式全22個 導出の流れつき 具体例で学ぶ数学



1から半角の公式の覚え方 使い方を解説 数学2bの苦手を克服 Studyplus スタディプラス




Cos15度を半角の公式を使って求めて欲しいです Clearnote




3倍角の公式の覚え方や証明は 入試問題付きでわかりやすく解説 東大医学部生の相談室




倍角公式半角公式 T 3 Sed




Sin Cos Tan 公式覚え方 三角比 三角関數の基礎sin Cos Tanが簡単に分かる解 Gkgnae




半角の公式の使い方 導出 覚え方 具体例で学ぶ数学



1から半角の公式の覚え方 使い方を解説 数学2bの苦手を克服 Studyplus スタディプラス




tan タンジェント の加法定理 倍角 半角 3倍角公式の覚え方 Youtube



半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法




半角の公式 覚え方 導き方 理系ラボ
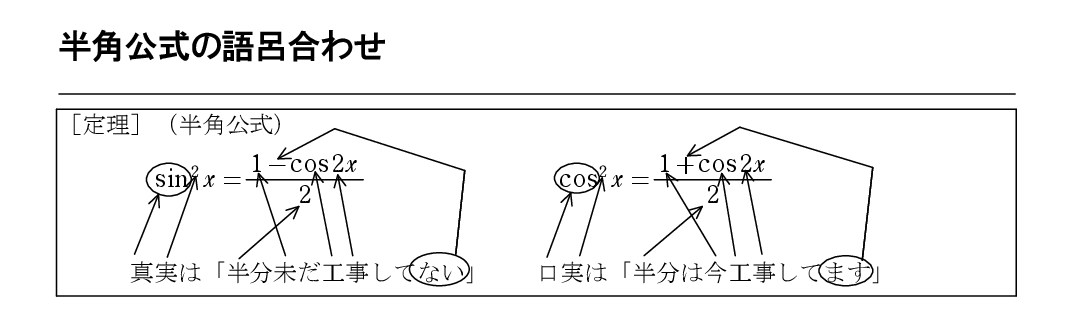



半角公式の語呂合わせ 怜悧玲瓏 高校数学を天空から俯瞰する




三角関数 の基本的な定理とその有用性を再確認してみませんか その2 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所
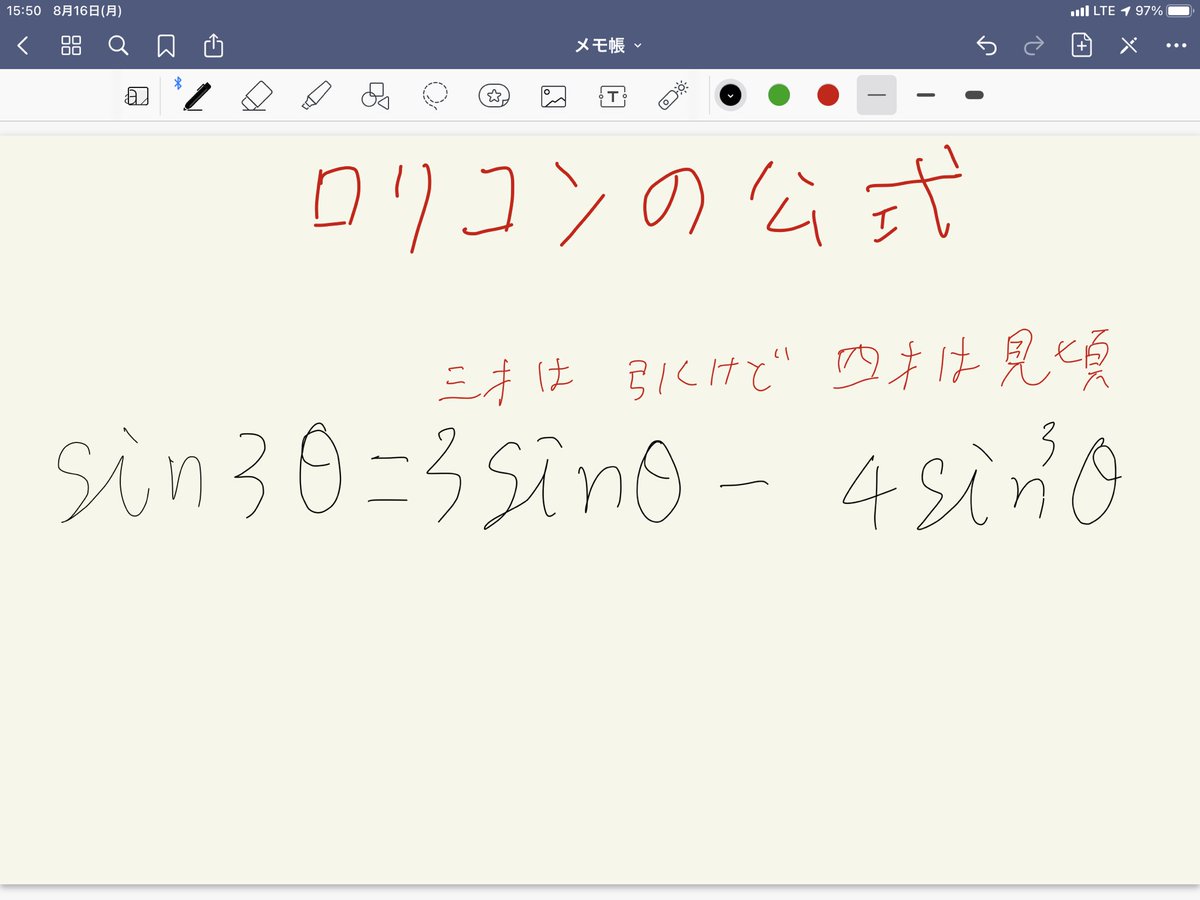



3倍角の公式




高2 加法定理は語呂合わせで完ペキに暗記 高校生 数学のノート Clearnote



2倍角の公式のすばらしい覚え方はありませんか 2倍角な Yahoo 知恵袋




下ネタ語呂 和積公式 積和公式の覚え方 Youtube




2倍角の公式と半角の公式 おいしい数学




数学ii 2倍角 半角の公式 三角関数の合成の証明 Mike先生のstudyブログ



2




半角の公式 覚え方 導き方 理系ラボ



0 件のコメント:
コメントを投稿